.MatheMagie / mathematische Zaubertricks MatheMagie (= Zauberkunststücke, die irgendwie und irgendwo und irgendwann mathematische Grundlagen besitzen, die man aber meist gar nicht merkt …)
auf dieser Seite: Aufstellung der „mathemagischen Bonbons“ von W. Hund
-Seite 1-
| Seiten | 1 | 2 | 3 |
Sie möchten bestellen? Tel. 09151/4716 oder gabys-zauberland@t-online.de oder über das Kontaktformular oben
Preisänderungen – leider! – vorbehalten. Mindestbestellsumme 15.- € + Porto Bezahlung mit PAYPAL möglich
Ladengeschäft: Amberger Str. 8 in 91217 Hersbruck (30 km östlich von Nürnberg); Öffnungszeiten Mo – Fr. 15.00 – 18.00 Uhr, Sa 10.00 – 13.00 Uhr (oder nach Vereinbarung!)
Eine Lehrerfortbildung in „Gabys Zauberland“? JAWOLL! DAS ist möglich und wurde in den letzten Jahren etliche Male durchgeführt! In den Bereichen „Zauberhafte Mathematik / MatheMagie“ und /oder „Physikalisches Spielzeug / physikalische Zaubereien“! Wir sind zwar räumlich beengt, aber bisher haben wir alle Seminare / Fachschaften so untergebracht, dass praktisch gearbeitet werden konnte! Eine bis zwei Stunden lang im wahrscheinlich einzigen Laden-Zaubergeschäft Deutschlands, das sich noch dazu auf diese Bereiche spezialisiert hat. Wichtig ist nur, dass Sie rechtzeitig vorher anfragen …: hund-hersbruck@t-online.de (= direkt zu Wolfgang Hund) VORFÜHREN würden wir z.B. unter anderem …
.
Der MATHEMAGISCHE Röntgenblick (Guess the total Cards) 9,00 € WIEDER DA!
 DAS ist ein Knüller besonders für MathematiklehrerInnen! Aber nicht nur für die! Auf fünf Karten sind vorne und hinten deutlich erkennbar verschiedene, einstellige Zahlen aufgedruckt. Ein Zuschauer steckt nun diese Karten beliebig gedreht in undurchsichtige Umschläge, so dass niemand die Zahlen mehr sehen kann. Die Vorführende hat sich dabei umgedreht oder das Zimmer sogar verlassen. Ist alles so geschehen, kann der /die MatheMagikerIn trotzdem die Summe der verdeckten Zahlen angeben, die nach oben gerichtet sind! Dies wird sofort überprüft: STIMMT! Eine Wiederholung kann ohne weitere Vorbereitung durchgeführt werden – mit einem anderen Endergebnis … WOW! Undurchschaubar, mit raffiniertem Trickhintergrund. Am besten ist es, wenn Sie sich das Demonstrationsvideo auf Youtube anschauen: http://funtimemagic.com/guess-the-total-cards Nicht für Kinder unter drei Jahren geeignet! Jetzt neu mit einer fantastischen Zusatzroutine, in der ein(e) Assistent(in) aus einem Nebenraum oder per Handy die Summe angeben kann, die er / sie nie gesehen hat! Unglaublich? Ist aber so …
DAS ist ein Knüller besonders für MathematiklehrerInnen! Aber nicht nur für die! Auf fünf Karten sind vorne und hinten deutlich erkennbar verschiedene, einstellige Zahlen aufgedruckt. Ein Zuschauer steckt nun diese Karten beliebig gedreht in undurchsichtige Umschläge, so dass niemand die Zahlen mehr sehen kann. Die Vorführende hat sich dabei umgedreht oder das Zimmer sogar verlassen. Ist alles so geschehen, kann der /die MatheMagikerIn trotzdem die Summe der verdeckten Zahlen angeben, die nach oben gerichtet sind! Dies wird sofort überprüft: STIMMT! Eine Wiederholung kann ohne weitere Vorbereitung durchgeführt werden – mit einem anderen Endergebnis … WOW! Undurchschaubar, mit raffiniertem Trickhintergrund. Am besten ist es, wenn Sie sich das Demonstrationsvideo auf Youtube anschauen: http://funtimemagic.com/guess-the-total-cards Nicht für Kinder unter drei Jahren geeignet! Jetzt neu mit einer fantastischen Zusatzroutine, in der ein(e) Assistent(in) aus einem Nebenraum oder per Handy die Summe angeben kann, die er / sie nie gesehen hat! Unglaublich? Ist aber so …
.
Neu 2023:
„Zauberwürfel“ 5 x 5 27,00 €
 Jetzt aber! In unserem Geschäft schaukeln sie sich gegenseitig hoch! Jugendliche aus dem benachbarten Gymnasium haben wirklich unglaubliches Geschick im Lösen der Rubik’sWürfel … und verlangten nach … : (Katalogtext) „Intelligentes, extra-kniffliges Geschicklichkeits-Geduld-Konzentrations-Spiel mit Spaßgarantie für schlaue Tüftler ab 7 Jahren. Der Würfel ist in Höhe, Breite und Tiefe in fünf Ebenen unterteilt. Diese lassen sich drehen. Dadurch können Position und Lage der verschiedenen Steine fast beliebig geändert werden. In der Grundstellung hat jede Seite des Würfels eine einheitliche, aber von Seite zu Seite unterschiedliche Farbe. Ziel ist es, den Würfel wieder in seine Grundstellung zu bringen, nachdem zuvor die Seiten in eine zufällige Stellung gedreht wurden. Achtung! Nicht geeignet für Kinder unter 36 Monaten.“
Jetzt aber! In unserem Geschäft schaukeln sie sich gegenseitig hoch! Jugendliche aus dem benachbarten Gymnasium haben wirklich unglaubliches Geschick im Lösen der Rubik’sWürfel … und verlangten nach … : (Katalogtext) „Intelligentes, extra-kniffliges Geschicklichkeits-Geduld-Konzentrations-Spiel mit Spaßgarantie für schlaue Tüftler ab 7 Jahren. Der Würfel ist in Höhe, Breite und Tiefe in fünf Ebenen unterteilt. Diese lassen sich drehen. Dadurch können Position und Lage der verschiedenen Steine fast beliebig geändert werden. In der Grundstellung hat jede Seite des Würfels eine einheitliche, aber von Seite zu Seite unterschiedliche Farbe. Ziel ist es, den Würfel wieder in seine Grundstellung zu bringen, nachdem zuvor die Seiten in eine zufällige Stellung gedreht wurden. Achtung! Nicht geeignet für Kinder unter 36 Monaten.“
„.
.
Spirograph 5,50 €

 Also, wenn das nicht „zauberhaft“, fast „magisch aussieht! Aus Holz, wunderbar gearbeitet. Von unserer Qualitätsfirma für Holzspielzeug GOKI; Zur Förderung der Kreativität und Auge-Hand-Koordination und für die Anfertigung toller Kunstwerke. Größe 13 x 13 cm, 6 Teile. MatheMagie … Nicht für Kinder unter drei Jahren.
Also, wenn das nicht „zauberhaft“, fast „magisch aussieht! Aus Holz, wunderbar gearbeitet. Von unserer Qualitätsfirma für Holzspielzeug GOKI; Zur Förderung der Kreativität und Auge-Hand-Koordination und für die Anfertigung toller Kunstwerke. Größe 13 x 13 cm, 6 Teile. MatheMagie … Nicht für Kinder unter drei Jahren.
.
.
.
.
..
Mit unsichtbaren Zahlen rechnen!(?!?) (Got your number) Sonderpreis 30,00 €
 Damit waren wir schnell zweimal ausverkauft, denn: Aufgrund der sauber gefertigten, bunten und deutlichen Requisiten kann dieses mathemagische „Wunder“ auch von einem größeres Publikum gut verfolgt werden: Der Vorführende zeigt fünf stabile Täfelchen vor (5,5 x 10 cm), die auf beiden Seiten verschiedene Zahlen enthalten, rote auf gelbem Untergrund und umgekehrt. Sie können nebeneinander in einen Ständer aus durchsichtigem und schwarzem (hochwertigen) Plexiglas (30x 7,5 x 2,7cm) gestellt werden, so dass die Zahlen in der Mitte vollständig verdeckt sind. Während sich der Vorführende umdreht (oder den Raum sogar verlässt), mischt ein Zuschauer die Zahlentafeln und dreht mehrere oder einzelne nach Belieben um. Dann stellt er sie in den Ständer, gemischt mit den roten oder gelben Seiten zum Publikum gerichtet. Die Zahlen sind völlig unsichtbar abgedeckt (wirklich!). Trotzdem kann der Mathemagiker z.B. mit Hilfe eines Pendels oder seiner „zahlenfühlenden Finger“ aus weiter Entfernung die Summe der verborgenen Zahlen angeben! Dies wird natürlich sofort überprüft: STIMMT! Bei einer eventuell geforderten Wiederholung ergibt sich ein anderes Ergebnis … Mathematisch erstaunlich einfach – aber trotzdem undurchschaubar und leicht vorzuführen! Neu mit extrem verblüffender Zuatzroutine, bei der ein(e) Assistent(in) sogar den Raum verlassen und von außen (!! auch über Handy!!) trotzdem die verdeckte Summe angeben kann! Echt! Wirklich! 🙂 🙂 Kein Kinderspielzeug!
Damit waren wir schnell zweimal ausverkauft, denn: Aufgrund der sauber gefertigten, bunten und deutlichen Requisiten kann dieses mathemagische „Wunder“ auch von einem größeres Publikum gut verfolgt werden: Der Vorführende zeigt fünf stabile Täfelchen vor (5,5 x 10 cm), die auf beiden Seiten verschiedene Zahlen enthalten, rote auf gelbem Untergrund und umgekehrt. Sie können nebeneinander in einen Ständer aus durchsichtigem und schwarzem (hochwertigen) Plexiglas (30x 7,5 x 2,7cm) gestellt werden, so dass die Zahlen in der Mitte vollständig verdeckt sind. Während sich der Vorführende umdreht (oder den Raum sogar verlässt), mischt ein Zuschauer die Zahlentafeln und dreht mehrere oder einzelne nach Belieben um. Dann stellt er sie in den Ständer, gemischt mit den roten oder gelben Seiten zum Publikum gerichtet. Die Zahlen sind völlig unsichtbar abgedeckt (wirklich!). Trotzdem kann der Mathemagiker z.B. mit Hilfe eines Pendels oder seiner „zahlenfühlenden Finger“ aus weiter Entfernung die Summe der verborgenen Zahlen angeben! Dies wird natürlich sofort überprüft: STIMMT! Bei einer eventuell geforderten Wiederholung ergibt sich ein anderes Ergebnis … Mathematisch erstaunlich einfach – aber trotzdem undurchschaubar und leicht vorzuführen! Neu mit extrem verblüffender Zuatzroutine, bei der ein(e) Assistent(in) sogar den Raum verlassen und von außen (!! auch über Handy!!) trotzdem die verdeckte Summe angeben kann! Echt! Wirklich! 🙂 🙂 Kein Kinderspielzeug!
.
.
.Die Zauberkette 8,00 €
 Lange verschwunden, jetzt wieder erhältlich! Ein Klassiker seit vielen Jahren: Der oberste Ring einer massiven Kette aus zwanzig Metallringen fällt blitzschnell durch die gesamte Kette nach unten! Ein optischer Schocker, da keiner der Ringe eine Öffnung hat! Metall dringt spurlos durch Metall (zumindest sieht es so aus)! Kein Zuschauer hat dafür auch nur im Ansatz eine Erklärung. Kein Kinderspielzeug! Das wird es nicht mehr geben, wenn unser Vorrat aufgebraucht ist …:-( In seinem bekannten Buch „Mathematische Zaubereien“ weist MatheMagie-Genie Martin Gardner auf Seite 92 auf dieses Kunststück hin: „Dem, was wir unter einem topologischen Trick verstehen, viel näher kommt ein Effekt, den der Zauberutensilienhandel gewöhnlich unter dem Namen „Purzelnde Ringe“ verkauft. Dabei handelt es sich um eine Reihe Ringe, die auf höchst merkwürdige Weise miteinander verbunden sind. Handhabt man sie richtig, so wir der Eindruck erweckt, als purzele ein Ring oben von der Kette herunter und verbinde sich mit dem untersten Ring … Das Purzeln ist jedoch eine durch mechanische Mittel hervorgerufene optische Illusion, die nicht auf topologischen Grenzen beruht…“ … (W.H.: Auf die man aber auch „reinfällt“, wenn man dies weiß!)
Lange verschwunden, jetzt wieder erhältlich! Ein Klassiker seit vielen Jahren: Der oberste Ring einer massiven Kette aus zwanzig Metallringen fällt blitzschnell durch die gesamte Kette nach unten! Ein optischer Schocker, da keiner der Ringe eine Öffnung hat! Metall dringt spurlos durch Metall (zumindest sieht es so aus)! Kein Zuschauer hat dafür auch nur im Ansatz eine Erklärung. Kein Kinderspielzeug! Das wird es nicht mehr geben, wenn unser Vorrat aufgebraucht ist …:-( In seinem bekannten Buch „Mathematische Zaubereien“ weist MatheMagie-Genie Martin Gardner auf Seite 92 auf dieses Kunststück hin: „Dem, was wir unter einem topologischen Trick verstehen, viel näher kommt ein Effekt, den der Zauberutensilienhandel gewöhnlich unter dem Namen „Purzelnde Ringe“ verkauft. Dabei handelt es sich um eine Reihe Ringe, die auf höchst merkwürdige Weise miteinander verbunden sind. Handhabt man sie richtig, so wir der Eindruck erweckt, als purzele ein Ring oben von der Kette herunter und verbinde sich mit dem untersten Ring … Das Purzeln ist jedoch eine durch mechanische Mittel hervorgerufene optische Illusion, die nicht auf topologischen Grenzen beruht…“ … (W.H.: Auf die man aber auch „reinfällt“, wenn man dies weiß!)
.
.
.Das Verflixte „T“ 2,00 €
 DANACH haben wir immer wieder gefragt, jahrelang vergeblich! Die kleine Ausführung haben wir ja noch, aber jetzt auch die 8x8x3 cm große, aus rotem Plastik. Mit mehr als 30 (!) Legemöglichkeiten und deren Lösungen! Kenner wissen das zu schätzen! Zahllose Unterrichtsstunden und Lehrerfortbildungen habe ich (W.H.) damit gestaltet, die jetzt noch in Erinnerung sind! Ein Klassiker der „Gehirnzerbröseler“! „Nur“ vier Teile, aus denen ein ganz einfaches „T“ zu legen ist! Wenn man „um’s Eck denkt! Eine halbe Stunde ist eine gute Zeit für die Lösung. Nicht für Kinder unter drei Jahren geeignet wegen verschluckbarer Kleinteile! Und auch nicht für Erwachsene mit geringer Frustrationstoleranz … Man kann damit auch wunderbar verschiedene LERNARTEN demonstrieren: Versuch und Irrtum – Nachahmendes Lernen – Einsichtiges Lernen! Jeweils nach einer Zeitspanne die nächste …
DANACH haben wir immer wieder gefragt, jahrelang vergeblich! Die kleine Ausführung haben wir ja noch, aber jetzt auch die 8x8x3 cm große, aus rotem Plastik. Mit mehr als 30 (!) Legemöglichkeiten und deren Lösungen! Kenner wissen das zu schätzen! Zahllose Unterrichtsstunden und Lehrerfortbildungen habe ich (W.H.) damit gestaltet, die jetzt noch in Erinnerung sind! Ein Klassiker der „Gehirnzerbröseler“! „Nur“ vier Teile, aus denen ein ganz einfaches „T“ zu legen ist! Wenn man „um’s Eck denkt! Eine halbe Stunde ist eine gute Zeit für die Lösung. Nicht für Kinder unter drei Jahren geeignet wegen verschluckbarer Kleinteile! Und auch nicht für Erwachsene mit geringer Frustrationstoleranz … Man kann damit auch wunderbar verschiedene LERNARTEN demonstrieren: Versuch und Irrtum – Nachahmendes Lernen – Einsichtiges Lernen! Jeweils nach einer Zeitspanne die nächste …
.
„Die Mathematik als Fachgebiet ist so ernst, dass man keine Gelegenheit versäumen sollte, dieses Fachgebiet etwas unterhaltsamer zu gestalten!“ (Blaise Pascal)
SONDERSERVICE: „Physikalische / chemische / mathematische Bonbons“ für Kunden von „Gabys Zauberland“ … Gesammelt, geschrieben, übersetzt, ausprobiert, verändert, gefunden von Wolfgang Hund („Hundini“) Diese Blätter können Sie bei einer Bestellung kostenlos erhalten: Für je 10.- € Warenbestellwert jeweils ein „Bonbon“. Sie können angeben, welche „Süßigkeiten“ Sie wollen … oder noch nicht haben …
Folgende „Bonbons“ befassen sich mit MatheMagischen Wundern: (die Gesamtaufstellung finden Sie auf der Physikseite 16!)
Nr. 8: Betrunkene Buchstaben! (?)Der / die Vorführende spricht übertrieben belehrend und mit penetrant erhobenem Zeigefinger über die berauschende Wirkung von Alkohol. Diese führe bekanntlich dazu, dass man nicht mehr richtig sehen könne und zum Beispiel meine, dass rosarote Elefanten, lila Kühe oder weiße Mäuse tatsächlich existieren würden. Mit Hilfe eines Spiegels könne man diesen seltsamen Effekt auch einfach demonstrieren, obwohl man keinen einzigen Tropfen Alkohol getrunken hat.
Nr. 11: Das Hufeisenspiel Ein Strategiespiel für zwei Spieler mit wenig Aufwand, aber großem Effekt! Jeder Spieler erhält 3 Spielsteine (Münzen, Muscheln, Bierdeckel, Radkappen, Kronkorken…) einer Farbe, die zum Anfang abwechselnd gesetzt werden. Das mittlere Feld muss zunächst frei bleiben. Beide Spieler ziehen nun abwechselnd auf den noch freien Punkt. Es darf nur entlang der Linien gezogen werden. Ist ein Spieler gefangen, kann also nicht mehr ziehen, hat er verloren.
Nr. 12: Wer trifft die 30? Sie rechnen gegen einen Zuschauer mit leichten Additionsaufgaben. Dabei verwenden Sie einen normalen Würfel. Den legen Sie immer abwechselnd mit einer gewählten Augenzahl auf den Tisch. Dann wird weiter zusammengerechnet. Wer die Zahl 30 genau erreicht, hat gewonnen … (wahrscheinlich, weil er das Geheimnis kennt …)
Nr. 13: Zahlentelepathie!?!?!? Ein Schüler schreibt ganz geheim eine dreistellige Zahl auf. Niemand außer ihm kennt sie! Wirklich nicht! Dann subtrahiert er die umgekehrte Zahlenreihenfolge und nennt vom Ergebnis die letzte Zahl. Mit (fast) übermenschlichen Fähigkeiten dringen Sie in sein visuelles Gedächtnis ein (denn er schaut sich die gesamte Differenz dabei an) und nennen die anderen beiden Zahlen des Ergebnisses. Dies kann sofort wiederholt werden …
Nr. 16: Mathematisches Hellsehen / TelepathieEin Zuschauer (oder eine ganze Gruppe, eine ganze Klasse, eine ganze Schule …) wählt frei (?) eine Zahl, führt einige Rechenoperationen aus, landet danach bei einem frei gewählten (?) Buchstaben und sucht sich völlig frei (?) bestimmte Tiere, Dinge, Länder …, die kurz notiert werden. Insgesamt werden sechs Begriffe aufgeschrieben, die eigentlich (?) niemand wissen kann! Schließlich konzentriert sich der Zuschauer (oder die Gruppe… s.o.) auf die fixierten Worte und sendet sie telepathisch der / dem übersinnlich Begabten. Die / der konzentriert sich … und nennt stockend die nur gedanklich übertragenen Begriffe …!
Nr. 17: Die Quersumme gewinnt oder verliert – wie SIE wollen!Ein Zuschauer setzt aus den Zahlen 1 – 2 – 3 – 4 – 5 und 6 zwei beliebige dreistellige Zahlen zusammen und addiert diese. Aus der Summe wird die einstellige Quersumme gebildet. Diese Zahl schließlich bestimmt einen von neun Briefumschlägen – und dann gewinnt der Zuschauer oder er verliert: Ganz wie der Vorführende es will!
Nr. 18: Das „………..“ – Phänomen! (Die „…..“ im Titel deshalb, weil Sie – wenn Sie denn „den Trick“ durchschaut haben – dieses mathematische Kartenwunder leicht auf IHRE speziellen Bedürfnisse umändern können: Den Namen Ihrer Schule, Ihren eigenen Namen, den eines Geburtstagskindes … usw.; erst DANN entfaltet dieses „Phänomen“ seine beste Wirkung! Ausprobieren – und immer wieder vorführen!
Nr. 19: Das 34 – Cent – MirakelDer / die Vorführende kündigt an, dass er / sie in der geschlossenen Hand einen bestimmten Geldbetrag verborgen hält, der nicht mehr verändert und erst zum Schluss gezeigt wird. Danach erhält ein Zuschauer ein Blatt mit einem Quadrat, das die Zahlen von 1 bis 16 enthält. Dazu kommen vier verschiedene Buntstifte. Der Helfer macht nun mit einem beliebigen Stift einen Kreis um eine der Zahlen und streicht alle anderen Zahlen im Feld durch, die senkrecht oder waagerecht zu dieser Zahl sind. Beispiel: Wird 6 umkreist, streicht er 5,7,8 (waagerecht) und 2,10,14 (senkrecht) mit der gleichen Farbe durch. Danach nimmt er einen anderen Stift, kreist von den übrig gebliebenen (also nicht durchgestrichenen) Zahlen eine ein und streicht wieder senkrecht oder waagerecht durch. Dasselbe noch mal. Die zuletzt nicht durchgestrichene Zahl wird ebenfalls umkreist. Jetzt wird noch einmal wiederholt, was bislang geschehen ist. Völlig freie Wahl der Zahlen und der Farben (die sind sowieso völlig egal, aber es sieht besser aus …!), weshalb auch eine „völlig frei entstandene Summe“ da ist, wenn man die eingekreisten Zahlen jetzt addiert … Wenn die Summenzahl bekannt und genannt ist, öffnet der Wundermann / die Mirakelfrau die Faust: Es sind genauso viele Centstücke darin, wie die Summe beträgt!!! WOW!!
Nr. 21: Wie viele Löcher gibt es? Ein quadratisches Papier wird mehrmals halbierend gefaltet. Auch wenn man noch so gut mitdenkt, rät man falsch auf die Frage, wie viele Löcher beim Abschneiden einer Ecke nach dem Auffalten sichtbar sind. Dies wird mit einer zweiten Ecke wiederholt – mit dem gleichen (falschen) Ergebnis!
Nr. 23: Ein Problem im Schullandheim – mathemagisch gelöst! Eine Sammlung von je acht männlichen und weiblichen Vornamen, durcheinander auf ein Blatt Papier geschrieben (das danach gefaltet wird), wird mit einem einzigen Scherenschnitt so geteilt, dass die Geschlechter getrennt sind! Einfacher, übersichtlicher Vorgang – ein umwerfender Effekt!
Nr. 26: Eine Würfelwette: „Psychokinetisch“ oder doch (nur) „mathematisch“?Sie wetten mit jemandem, dass Sie normale Würfel beim Wurf mit ihren Gedanken so beeinflussen können, dass bestimmte Augenzahlen häufiger vorkommen, als andere. Das kann doch eigentlich nur Psychokinese sein (= Bewegen oder Verformen von Gegenständen durch Gedankenkraft). Oder?Zum Beweis wird dieser Vorgang mit zwei Würfeln zwanzig mal durchgeführt, mit den Zahlen 2 und 6. Jedesmal wird protokolliert, ob es Ihnen gelang, eine 2 oder eine 6 zu erzwingen. Nach 20 Würfen wird gezählt: Tatsächlich haben Sie gewonnen … ! Dies kann auch mit anderen Zahlen wiederholt werden.
Nr. 27: Ich bin „Zahlenschwingungssensibler“ (ZSS)! (?????) Dieses Kunststück ist ein absoluter KNÜLLER! Nicht weitersagen! Fünf Karten enthalten Zehnerzahlen auf der Vorder- und Rückseite. Rote und blaue. Ein Zuschauer mischt und dreht die Karten beliebig um, bevor er sie auf dem Tisch in einer zufälligen Reihe auslegt. Die (roten und blauen) Zahlen werden mit einem dicken Kartonstreifen oder einer Holzleiste abgedeckt, so dass sie nicht mehr sichtbar sind. Bei allen diesen Vorgängen befindet sich der „Zahlenschwingungssensible“ (ZSS) nicht im Raum oder außer Sicht in einer Ecke. Ist alles erledigt, hält der ZSS ein Pendel über die unsichtbare Zahlenreihe, „um die Schwingungen zu speichern“. Wenn das Pendel anschließend über mögliche Summen gehalten wird, schlägt es über der richtigen (= der verborgenen) aus! Das kann beliebig oft wiederholt werden!
Nr. 32: Der besiegte Zufall Der Name dieses (zunächst immer) unglaublichen Kunststückes stammt von einem der renommiertesten Zaubermeister Deutschlands, Jochen Zmeck. „Es gibt nur wirklich wenige Kartentricks, die „ganz von selbst“ gehen und dabei trotzdem noch effektvoll sind. Hier ist einer. Und wenn Sie noch nie einen Kartentrick gezeigt haben und auch nie einen weiteren zeigen werden, diesen können Sie sich einprägen und wieder und immer wieder vorführen. Nur ein ganz kluger Mathematiker wird hinter das Geheimnis kommen.“
Nr. 34: „DAS glaub‘ ich nicht! Her mit dem Würfel! Mit einem normalen Würfel führt ein Zuschauer nach zwei einfachen Regeln Bewegungen durch. Obwohl er die Ausgangszahl völlig frei wählen durfte und der Vorführende nichts sieht, kann die zum Schluss oben liegende Zahl genannt werden! Das glaubt man nicht, bevor man es nicht selbst mehrere Male gemacht hat!
Nr. 37: Geheimnisvolle Würfel (MatheMagie): Obwohl sich der Vorführende abgewendet hatte oder sogar den Raum verließ, kann er angeben, welche Zahlen bei zwei von einem Zuschauer geworfenen Würfeln oben liegen!
Nr. 43: Nostalgische MatheMagie pur! – Der sichere Spielgewinn Solange Sie das nicht ausprobiert haben, glauben Sie nicht, dass überhaupt und wie leicht dieses durch und durch mathemagische Kunststück funktioniert und wie groß die Verblüffung und Verzweiflung (nicht hinter das Geheimnis zu kommen) des betreffenden Publikums sein wird! Bereits 1900 wurde es vom deutschen Zauberkünstler Carl Willmann in seiner „Magischen Bibliothek“ im 3. Band „Magische Gesellschaftsspiele“ veröffentlicht. Und das war bestimmt nicht der Anfang … (und nicht das Ende … )
Nr. 45: 42 378 594 oder auch anders …Eine zufällig ausgewählte große Zahl wird zunächst in Zahlen, dann in Worten geschrieben. Die dabei entstandene Buchstabenzahl wird wieder in Zahlen festgehalten und dann ausgeschrieben. So geht es weiter, bis zu einer Zahl, bei der es erkennbar zuende ist. Diese so willkürlich gefundene Zahl bestimmt eine Spielkarte, die rückenoben in einem Kartenstoß liegt. Wird diese „völlig frei bestimmte Karte“ umgedreht, befindet sich auf ihrer Vorderseite ein Aufkleber:„Prima! Toll gemacht! Du wirst diese Karte wählen!“ Unnötig zu sagen, dass dies die einzige markierte Karte des ganzen Stoßes ist … !!! WOW!
Nr. 46: MatheMagische Zauberwörter!(?) Mit einem normalen Kartenspiel (Schwarzer Peter, Quartett, Skat, Poker …) geschieht ein schier unglaublicher, undurchschaubarer Effekt, ohne dass SIE dieses Spiel überhaupt in die Hand nehmen müssen! Das bedeutet wirklich, dass Sie sich mit verschränkten Armen in einen Sessel kuscheln und nur mit Ihrem magischen Denken bzw. den daraus resultierenden Anweisungen agieren können! Wirklich! 😉
Nr. 48: Eine magische Uhrzeit (MatheMagie): Ein Zuschauer denkt sich eine Uhrzeit. Auf undurchschaubare (mathemagische) Weise wird diese schnell und sicher herausgefunden!
Nr. 50: Ein verzwicktes Bruchrechnen mit Pferdeteilen!(MatheMagie) Bei der Bonbon-Jubiläumsausgabe wird eine seit Generationen beliebte, sehr verblüffende, einfach zu verstehende, aber schwer zu durchschauende Denksportaufgabe gestellt, die es in vielen Variationen gab. Heute leider nur noch wenig bekannt …
Nr. 56: Die Lieblingszahl erscheint „zauberhaft“ (MatheMagie) Die einstellige Lieblingszahl eines Zuschauers erscheint nach einer magischen Rechenoperation gleich vielfach als Ergebnis!
Nr. 58: Blitzschnelles Kopfrechnen! (MatheMagie) Fünf sechseckige Scheiben enthalten je sechs verschiedene dreistellige Zahlen. Wer das Geheimnis kennt, kann blitzschnell fünf frei gewählte Zahlen im Kopf addieren!
Nr. 61: Zwei verhexte, verzwickte … unlösbare Sachaufgaben? …(MatheMagie) … „Gehirnzerbröselung“ bei Jung und Reif …
Nr. 63: MatheMagische Streichholzbonbons(MatheMagie): Ein Plädoyer für Streichholztüfteleien, mit vier besonders guten Beispielen.
Nr. 64: Die mathemagische 6 (oder 9)!(MatheMagie) Eine völlig frei gewählte Zahl führt einen Zuschauer zwingend zu einem Tier, das die Vorführende schon vorher aufgeschrieben hat! MatheMagie pur, umwerfender Effekt (auch für Erwachsene).
Nr. 65: Drinnen oder draußen? … Magische Topologie halt … (MatheMagie) „Das Strumpfband des Riesen“ hieß dieser wunderbare Effekt früher schon, den man mit einer Schnur auf dem Tisch oder einem Seil auf dem Boden durchführen kann. Beste Unterhaltung für eine ganze Gesellschaft – und doch so mathemagisch …
Nr. 66: Mit einer Linie? Unmöglich!(MatheMagie) In Abwandlung des bekannten „Haus des Nikolaus“ sollen Figuren ebenfalls mit einer Linie gezeichnet werden. Manchmal geht es leicht, manchmal schwer … – und manchmal gar nicht! Warum bloß …?
Nr. 67: Hand- und kopfgemachte MatheMagie! (MatheMagie) Mit einem (noch hand- und kopfgemachten) Zahlenquadrat, das aus 225 (!) bunt gemischten Zahlen besteht, werden unglaubliche, „magisch“ anmutende Additionen durchgeführt.
Nr. 71: „Pech gehabt!“ (oder auch „Glück“, wenn SIE wollen …) MatheMagie Ein Zuschauer bildet zwei dreistellige Zahlen, die er addiert. Die Quersumme führt ihn entweder zu einem Briefumschlag mit Geld oder zu einer Niete … MatheMagische Unterhaltung auch für ein größeres Publikum!
Nr. 72: Wer arbeitet üüüüberhaupt noch? (außer IHNEN natürlich …)MatheMagie Sie beweisen „mathematisch zwingend, eindeutig logisch, übersichtlich und anschaulich“, dass eigentlich niemand mehr arbeitet …
Nr. 73: Gewusst wie! Lehrer sind findige Leute …! MatheMagie Eine Geschichte aus dem Schulalltag, die zunächst völlig schlüssig klingt, dann aber mit einem „unmöglichen2 Schluss endet. Wo ist der logische Knax?
Nr. 74: Wer kann bis 10 zählen? (na ja, wer denn nicht? .. Denkste!)Die Lehrkraft kann mit drei Gegenständen bis 10 zählen. Kein Schüler kann dies (auf Anhieb) nachmachen …
Nr. 75: Wer kann das nachmachen? („Babyleicht!!“ – Nur zu …!) MatheMagie Sie führen einige einfache Kartenbewegungen auf dem Tisch mit sechs Spielkarten durch. Niemand kann das nachmachen!
Nr. 76: Heute ist Zahltag! MatheMagie Sie können mit vorab ausgefüllten (!) Schecks jeden gewünschten Betrag bis 1000.- € auszahlen…
Nr. 77; Kannst du richtig zählen? lustige MatheMagie Ein überraschendes Zähl“experiment“ für Kinder, Jugendliche und Erwachsene
Nr. 82: „Ich schenke dir 5 Euro!“(MatheMagie) Ein Zuschauer versucht, mit einer völlig frei gewählten Zahl den einzigen Briefumschlag mit einem Geldschein aus einem Stoß mit leeren Umschlägen auszuzählen! Vergeblich … 🙂 Mathemagie pur!
Nr. 83: Eine unmögliche Faltfigur – Hyper Card(MatheMagie) Eine „unmögliche Figur“ steht auf dem Tisch und fordert zum Nachdenken, Stutzen, Stauen und – zum Nachmachen auf! Ein mathemagischer Knüller …!
Nr. 84: Das „Pony-Rätsel“ von Sam Loyd(MatheMagie) Ein Gehirnzerbröseler, der schon Generationen beschäftigte …
Nr. 85: Ein verflixtes Denkspiel aus dem 18. Jahrhundert (MatheMagie) „Easy! Babyleicht! Keine Kunst! …“ Nur zu … 😉 🙂
Nr. 86: Wohin geht es dieses Jahr in den Urlaub? (MatheMagie) Mit einer frei gewählten Zahl werden verschiedene, einfache Rechenoperationen durchgeführt. Das Ergebnis wird eine (zumindest im Jahr 2020) erstaunlich treffsichere Prophezeiung sein im Hinblick auf das Urlaubsziel!
Nr. 88; Eine mathemagische Wohnung!(MatheMagie) Ein Zuschauer wählt „mathemagisch“ ein Zimmer auf einem Wohnungsgrundriss aus, „völlig frei“ – trotzdem kann die / der GeheimnisträgerIn selbst am Telefon oder per Mail erkennen, in welchem Raum er sich befindet!
Nr. 91: „Zaubern“ mit Kreisdurchmesser und Kreisumfang(MatheMagie) Eine Münze durchdringt ein Loch in einem Blatt Papier, das dafür eigentlich viel zu klein ist! Aufgrund der mathematischen Formeln ist dies aber klar …
Nr. 92: Zahlen, Zahlen, Zahlen überall … (Superallgemeintest!):mit diesem Blatt beschäftigen Sie Menschen ab 10 Jahren stunden-, tage, wochenlang! Sehr bewährt … 😉
Nr. 94: MatheMagische Scherenbefreiung(Mathe) Eine doch eigentlich unlösbar mit einer Schnur gefesselte Schere wird schnell befreit, obwohl ein Zuschauer die Enden festhält!
Nr. 95: Unbewusste Zahlentelepathie(MatheMagie) Eine undurchschaubare mathemagische Perle, bei der eine völlig frei gewählte Zahl gedanklich empfangen wird!
Nr. 96: MatheMagie mit drei Würfeln 1 (MatheMagie) Drei Personen würfeln mit drei Würfeln, ohne dass es die Vorführende sieht. Dann wird mehrmals addiert und multipliziert. Aus dem Schlussergebnis kann die MatheMagierin angeben, welche Zahlen jeweils bei jeder Person am Anfang gewürfelt wurden!
Nr. 97: MatheMagie mit drei Würfeln 2: (MatheMagie) Ein Helfer würfelt mit drei Würfeln und führt dann einige verwirrende mathematische Operationen durch. Ein Blick auf die Schlusskonstellation der drei Würfel – und das Gesamtergebnis kann angegeben werden!
Nr 98: MatheMagie mit drei Würfeln 3: (MatheMagie) Ein Helfer baut einen Turm aus 3 (oder mehr) Würfeln und bedeckt ihn mit einer passenden, undurchsichtigen Hülse. Trotzdem kann man mit einem „mathematischen Röntgenblick“ angeben, wie … (auch schon für Grundschulkinder geeignet!)
Nr. 99: Mathemagische Verbindungen zwischen Würfel, Papier und Schere (MatheMagie) Der Vorführende faltet ein quadratisches Papier, während eine Zuschauerin einen normalen Spielwürfel wirft. Wird das Papier entfaltet, enthält es genau so viele Löcher wie …! Dies kann wiederholt werden!
103: „Wer zahlt die Zeche beim Lehrerausflug?“ (MatheMagie) Auf lustige, überraschende, unverstänldiche, zufällige, magische Weise übernimmt die Schulleitung die gesamt Zeche beim Lehrerausflug! Eine Perle der MatheMagie … 😉
104: „Ist doch logisch! Kinderleicht! Kein Problem!“ — „Upps! DOCH eines …!“ (Logik / Wahrnehmung) Eine einfache Handlung mir drei Gläsern soll sofort nachgemacht werden. Daran scheitern aber die allmeisten …. 😉 Ein klassischer Nervtöter!
105: Mit Logik und kreativem Denken geht das Licht an! (Logik / Kreativität) Es wird ein Rätsel gestellt, das eigentlich unmöglich mit der gestellten Bedingung gelöst werden kann! Und doch ist es möglich … (zwei Fassungen: Eine mit, eine VORERST ohne Lösung!)
106: DAS kann ja wohl nicht sein! „Wo ein Körper ist, … usw.“ (Physik? Magie? Logik? ___?) Auf einer normalen Nähnadel sind sechs bis zehn Fäden durch das winzige Öhr gezogen! Ein unglaubliches Phänomen, das man zum Untersuchen hergeben kann …
107: Ein mathemagischer Gruppenschocker! (MatheMagie) Eine Gruppe / Schulklasse rechnet mit frei gewählten Ausgangszahlen verschiedene Operationen – und gelangt doch zum gleichen Ergebnis! WOW!
108: Wer kann das nachmachen? (MatheMagie / Logisches Denken) Ein Nervtöter auch für Erwachsene: Mit nur 6 Spielkarten sollen einige Bewegungen nachgemacht werden. Einfach? Denkste!
109: Volltreffer aus 331776 Möglichkeiten! (MatheMagie) Der Titel sagt alles: Eine Perle der MatheMagie, die genauso gut zur reinen Unterhaltung wie zur unterrichtlichen Auswertung und Ausweitung eingesetzt werden kann! Wenig Aufwand – Riesenerfolg!
110: Die mathemagische Färbung eines Stiftes! (MatheMagie) Ein erschlagendes Phänomen, das Laien und Tüftel-/Mathe-Profis aller Altersgruppen lange beschäftigen kann – meist ohne, dass es zu einer Lösung kommt!
111: MatheMagisches Geldverschwinden! (MatheMagie) In einer übersichtlichen Sachsituation verschwindet mathemagisch ein Geldbetrag! Dies sorgt auch bei Gruppen von z.B. Lehrkräften für heftige Diskussionen …! 😉
112: Männer werden zu Biergläsern! Oder umgekehrt … (MatheMagie) Obwohl sich DAS schon einige Leute gedacht haben, kann dieses mathemagische Phänomen nicht gleich als „Beweis“ dafür herangezogen werden! Oder vielleicht doch? … 😉
113: Die Urmutter der MatheMagie: Die Goetheschen Zahlentafeln! (MatheMagie) Der Titel sagt eigentlich schon alles, aber hier noch mit Anregungen aus hundertfacher „zauberhafter“ Vorführung …!
114: Das zauberhafte Maßband! (MatheMagie) Mit einem normalen Schneider- Maßband kann man unglaubliche mathemagische Kunststücke vorführen.
115: Wie der Phönix aus der Asche: Die zyklische Zahl! (MatheMagie) Zauberei mit der phänomenalen zyZa … 😉 Anregungen aus der Praxis
116: Topologische Zaubereien: Das Papierrennen á la Möbius (MatheMagie) Eine vielfach bewährte Vorführmethode dieses mathematischen Phänomens, die sogar für die Bühne oder andere große Veranstaltungen geeignet ist!
120: Von „babyleicht“ bis „(fast) unmöglich“! (MatheMagie) Mit nuuuur sechs Puzzleteilen sollen stufenweise Quadrate gelegt werden. Anfangs eben „babyleicht“, aber daaaaaannnn … 😉
121: Die Quadratur der Kreise (MatheMagie): Was Mathematiker seit Urzeiten immer wieder beweisen wollen, kann mit MatheMagie unterhaltsam und anschaulich „bewiesen“ werden!
122: Wer nimmt den letzten Stein? (MatheMagie): Ein Klassiker der unterhaltsamen, tüfteligen Denkspiele, den man ohne große Vorbereitungen überall präsentieren kann (Kindern, Jugendlichen und Erwachsenen)!
UND, nur mal so nebenbei erwähnt: DIESES Geschäft wird es nicht mehr geben (können), wenn die in der Person von Wolfgang Hund sich im Lauf der vielen Jahren zufällig vereinten (mathematisch-didaktischen) Kenntnisse, (zauberischen) Fähigkeiten und Geschäftsverbindungen (nach USA, Indien …) nicht mehr vorhanden sind. Wir alle wissen, wie schnell sich Verhältnisse ändern können. Momentan (Dezember 2023) denken wir nur selten an ein Aufhören, aber natürlich ist es mit 75 Jahren irgendwie schon am Horizont … Halten Sie dies bitte im Hinterkopf, wenn Sie unser Sortiment durchstöbern! Viele der angebotenen Artikel wird es wahrscheinlich in Ihrer „Reichweite“ nie mehr geben können …
.
Teufelsschlinge CHINESISCHES ESSSTÄBCHEN 4,00 €
 Genau für DIESES Teufelsding gilt das oben Gesagte besonders! Mir (W.H.) ist heute noch, nach Jahrzehnten (!), ein konkreter Schüler einer 7. Klasse im Gedächtnis, dem ich die Teufelsschlinge am Montagmorgen ans Hemd knöpfte (blitzschnell übrigens) – und dann lief er bis Freitagmittag damit rum! Er wollte sich nicht befreien lassen, sondern es selbst schaffen (auch daheim): Vergeblich! Dabei handelt es sich nicht um einen TRICK, sondern um ein mathematisch – topologisches Problem. Wenn man es ein paarmal gemacht hat, geht das Dran- und Abmachen flott! Und dieses Stäbchen ist 26,5 cm lang (!!!), mit chinesischen Schriftzeichen. WIR legen Ihnen freundlicherweise eine Beschreibung bei, die unser Lieferant „vergessen“ hat … 😉 Kein Kinderspielzeug, erst recht nicht für Menschlein unter drei Jahren – logisch!
Genau für DIESES Teufelsding gilt das oben Gesagte besonders! Mir (W.H.) ist heute noch, nach Jahrzehnten (!), ein konkreter Schüler einer 7. Klasse im Gedächtnis, dem ich die Teufelsschlinge am Montagmorgen ans Hemd knöpfte (blitzschnell übrigens) – und dann lief er bis Freitagmittag damit rum! Er wollte sich nicht befreien lassen, sondern es selbst schaffen (auch daheim): Vergeblich! Dabei handelt es sich nicht um einen TRICK, sondern um ein mathematisch – topologisches Problem. Wenn man es ein paarmal gemacht hat, geht das Dran- und Abmachen flott! Und dieses Stäbchen ist 26,5 cm lang (!!!), mit chinesischen Schriftzeichen. WIR legen Ihnen freundlicherweise eine Beschreibung bei, die unser Lieferant „vergessen“ hat … 😉 Kein Kinderspielzeug, erst recht nicht für Menschlein unter drei Jahren – logisch!
Knopflochstab Bleistift recycled 4,00 €
 Wie oben, als 17 cm langer Bleistift …
Wie oben, als 17 cm langer Bleistift …
.
.
.
.
GANZ NEU! GANZ TOLL!DAS gibt es WELTWEIT NUR BEI UNS! Wir sind sehr stolz, dass wir es geschafft haben und danken dem Rechteinhaber in Indien für die Überlassung dieser beiden Wunderwerke!
Zwei mathemagische Zauberrätsel, die einzelne Personen oder ganze Gruppen stunden- / tage- /wochenlang beschäftigen!
1.Welcher Mann verschwindet durch Umlegen der beiden oberen Teile? Wo geht er hin? Was macht er dort? Wann kommt er wieder? Und warum und überhaupt? Man muss seine VERMUTUNGEN aber BEWEISEN!
2. Welcher ROTE Stift verwandelt sich in einen BLAUEN? Nur durch Umlegen der beiden unteren Teilen!
Sonderpreis für einen A4 – Bogen mit je drei 3,50 € Bitte geben Sie an, welches Motiv Sie wollen: Männer oder Stifte …
.
.
. . .
.
.
Gozinta Boxes (groß) 18,00 €
 Eine schwarze, „würfelförmige“ Schachtel, ca. 13 cm 😉 wird geöffnet und eine darin befindliche rote Box herausgenommen (oder umgekehrt). Logisch, dass also der schwarze Behälter größer sein muss, als der rote. Logisch? Na ja … denn jetzt wird die rote Schachtel geöffnet, die schwarze geschlossen … und in die rote gesteckt. Deckel drauf … und gestaunt! Ist doch eigentlich unmöglich, oder? Das können Sie wiederholen, so oft Sie wollen. Mal ist die eine Box „größer“, mal die andere! Obwohl beide objektiv gesehen genau gleich groß sind! Ehrlich! Ein räumliches Paradoxon, das einen verrückt machen kann. Kein Kinderspielzeug! Schauen Sie sich mal die entsprechenden YouTube-Videos an!
Eine schwarze, „würfelförmige“ Schachtel, ca. 13 cm 😉 wird geöffnet und eine darin befindliche rote Box herausgenommen (oder umgekehrt). Logisch, dass also der schwarze Behälter größer sein muss, als der rote. Logisch? Na ja … denn jetzt wird die rote Schachtel geöffnet, die schwarze geschlossen … und in die rote gesteckt. Deckel drauf … und gestaunt! Ist doch eigentlich unmöglich, oder? Das können Sie wiederholen, so oft Sie wollen. Mal ist die eine Box „größer“, mal die andere! Obwohl beide objektiv gesehen genau gleich groß sind! Ehrlich! Ein räumliches Paradoxon, das einen verrückt machen kann. Kein Kinderspielzeug! Schauen Sie sich mal die entsprechenden YouTube-Videos an!
In & Out – Boxes 8.- €  Die Wunderboxen aus stabilem Plastik gibt es auch! Mit deutscher Beschreibung. Die Maße der Würfel (mmh…) betragen dann, wenn der andere Würfel (mmh…) drin steckt: 4,5 cm x 4 cm x 4,5 cm (mmh …); egal, welche Farbe sich wo befindet (mmh…) – darüber muss ich noch mal nachdenken – irgendwas stimmt da nicht … mmh …
Die Wunderboxen aus stabilem Plastik gibt es auch! Mit deutscher Beschreibung. Die Maße der Würfel (mmh…) betragen dann, wenn der andere Würfel (mmh…) drin steckt: 4,5 cm x 4 cm x 4,5 cm (mmh …); egal, welche Farbe sich wo befindet (mmh…) – darüber muss ich noch mal nachdenken – irgendwas stimmt da nicht … mmh …
Nur sicherheitshalber: Nicht geeignet für Kinder unter drei Jahren …
.
.
Und hier kommt die zauberhafte Anwendung, die bei einer Fortbildung für Seminarlehrer (Mathematik) fast für stehende Ovationen sorgte: Weltexklusiv bei uns …!
Exklusivtrick! Die paranormalen Garagenautohasen!Sonderpreis 18.- €!  Zwei gleich große, offensichtlich leere, „würfelförmige“ Plastikschachteln (rot und schwarz) sollen eine Garage und ein Auto symbolisieren. Die rote Schachtel (= das Auto) kann in die schwarze (= die Garage) gesteckt werden. Gleich darauf passiert aber genau das Umgekehrte! (= die in Zaubererkreisen bekannten „In–and-Out–Boxen“, s.o.). Die schwarze wird nun in die rote Box gesteckt! Die Ursache für diesen verblüffenden Vorgang soll angeblich ein roter Ball sein, der jeweils das „Schrumpfen“ besorgt. Je nachdem, in welcher Schachtel er sich befindet, wird diese kleiner, so dass sie in die andere gesteckt werden kann. Dies wird mehrmals wiederholt. Dann wird dieser magische Ball auf die Seite gelegt und ein Zuschauer kann selbst bestimmen, welche Box in welche soll. Merkwürdiger Weise funktioniert auch dies. Wird aber danach die innere Schachtel wieder herausgeholt und geöffnet, befindet sich in ihr plötzlich ein roter Schaumstoffhase!!! Nun wird die vorher äußere (= größere) Box geschlossen und in die vorher innere (= kleinere) gesteckt: Auch dies gelingt! Wird dann erneut die innere Schachtel geöffnet, befindet sich auch in ihr ein Schaumstoffhase! Die Zuschauer sind zu Recht schon fix und fertig! Nun aber nimmt der Vorführende den roten Ball vom Anfang auf, legt ihn auf eine Faust und stößt ihn langsam mit dem Zeigefinger der anderen Hand hinein. Langsam wird die Faust geöffnet: In ihr befindet sich ein roter Riesenhase, der eigentlich weder in die Hand noch in die Schachteln reinpasst! Ein echter Schocker, der langsam, mit nackten Händen und Armen, notfalls in der Badehose, vorgeführt werden kann! Bei fast jeder Vorführung im Geschäft hieß es: „Möchte ich auch haben!“ Und ehrlich: Sie brauchen keine „besonderen magischen Fähigkeiten“, um dieses Wunder vorführen zu können! Mal ehrlich: Die zweite „Staffel“ ist verkauft und eigentlich wollten wir nicht mehr … Die Corona-Virus-Flaute daheim hat aber noch mal eine neue Menge in geringer Stückzahl im Wohnzimmer entstehen lassen (mit 15 Einzelschritten schon ziemlich mühsam!). „Unsicher ist, ob nochmal dergleichen!“ (würde Meister Yoda sagen) Achtung: Nicht geeignet für Kinder unter drei Jahren wegen verschluckbarer Kleinteile! Allgemein kein Kinderspielzeug!
Zwei gleich große, offensichtlich leere, „würfelförmige“ Plastikschachteln (rot und schwarz) sollen eine Garage und ein Auto symbolisieren. Die rote Schachtel (= das Auto) kann in die schwarze (= die Garage) gesteckt werden. Gleich darauf passiert aber genau das Umgekehrte! (= die in Zaubererkreisen bekannten „In–and-Out–Boxen“, s.o.). Die schwarze wird nun in die rote Box gesteckt! Die Ursache für diesen verblüffenden Vorgang soll angeblich ein roter Ball sein, der jeweils das „Schrumpfen“ besorgt. Je nachdem, in welcher Schachtel er sich befindet, wird diese kleiner, so dass sie in die andere gesteckt werden kann. Dies wird mehrmals wiederholt. Dann wird dieser magische Ball auf die Seite gelegt und ein Zuschauer kann selbst bestimmen, welche Box in welche soll. Merkwürdiger Weise funktioniert auch dies. Wird aber danach die innere Schachtel wieder herausgeholt und geöffnet, befindet sich in ihr plötzlich ein roter Schaumstoffhase!!! Nun wird die vorher äußere (= größere) Box geschlossen und in die vorher innere (= kleinere) gesteckt: Auch dies gelingt! Wird dann erneut die innere Schachtel geöffnet, befindet sich auch in ihr ein Schaumstoffhase! Die Zuschauer sind zu Recht schon fix und fertig! Nun aber nimmt der Vorführende den roten Ball vom Anfang auf, legt ihn auf eine Faust und stößt ihn langsam mit dem Zeigefinger der anderen Hand hinein. Langsam wird die Faust geöffnet: In ihr befindet sich ein roter Riesenhase, der eigentlich weder in die Hand noch in die Schachteln reinpasst! Ein echter Schocker, der langsam, mit nackten Händen und Armen, notfalls in der Badehose, vorgeführt werden kann! Bei fast jeder Vorführung im Geschäft hieß es: „Möchte ich auch haben!“ Und ehrlich: Sie brauchen keine „besonderen magischen Fähigkeiten“, um dieses Wunder vorführen zu können! Mal ehrlich: Die zweite „Staffel“ ist verkauft und eigentlich wollten wir nicht mehr … Die Corona-Virus-Flaute daheim hat aber noch mal eine neue Menge in geringer Stückzahl im Wohnzimmer entstehen lassen (mit 15 Einzelschritten schon ziemlich mühsam!). „Unsicher ist, ob nochmal dergleichen!“ (würde Meister Yoda sagen) Achtung: Nicht geeignet für Kinder unter drei Jahren wegen verschluckbarer Kleinteile! Allgemein kein Kinderspielzeug!
.
Das Eselpuzzle (Donkey Puzzle)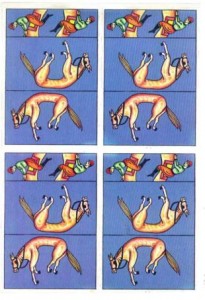 DAS gibt es in ganz Europa nur bei uns!Ein A 4 – Kartonbogen mit vier der berühmten Nervtöterpuzzles von Sam Loyd. Mit diesem raffinierten Legerätsel wurde Loyd Millionär! Es besteht nur aus drei Teilen („Muss ja babyleicht sein!“, sagen vor allem Kinder und Jugendliche, Erwachsene denken sich das …). Das Ziel ist, durch das Legen dieser Kartonstreifen die Reiter auf die Esel zu setzen. Na ja, eigentlich sind es ja Maulesel. Jeder Reiter sitzt so auf einem Tier, wie man halt draufsitzt! Wir bieten Ihnen einen A 4 – Bogen zum Ausschneiden an, der gleich vier Puzzles enthält! Also ideal für Gruppen oder als verblüffendes Geschenk! Staffelpreise: 1 – 9 Bögen: 2.- € pro Bogen 10 – 19 Bögen: 1,80 € 20 – 49 Bögen: 1,60 € ab 50 Bögen: 1,40 € Schlagen Sie zu, solange unser Vorrat reicht!
DAS gibt es in ganz Europa nur bei uns!Ein A 4 – Kartonbogen mit vier der berühmten Nervtöterpuzzles von Sam Loyd. Mit diesem raffinierten Legerätsel wurde Loyd Millionär! Es besteht nur aus drei Teilen („Muss ja babyleicht sein!“, sagen vor allem Kinder und Jugendliche, Erwachsene denken sich das …). Das Ziel ist, durch das Legen dieser Kartonstreifen die Reiter auf die Esel zu setzen. Na ja, eigentlich sind es ja Maulesel. Jeder Reiter sitzt so auf einem Tier, wie man halt draufsitzt! Wir bieten Ihnen einen A 4 – Bogen zum Ausschneiden an, der gleich vier Puzzles enthält! Also ideal für Gruppen oder als verblüffendes Geschenk! Staffelpreise: 1 – 9 Bögen: 2.- € pro Bogen 10 – 19 Bögen: 1,80 € 20 – 49 Bögen: 1,60 € ab 50 Bögen: 1,40 € Schlagen Sie zu, solange unser Vorrat reicht!
.
.
.
.
.
Die kopflose Dame(Headless Lady)
 DAS gibt es in ganz Europa nur bei uns! Ein A 4 – Kartonbogen mit vier Exemplaren einer mathematischen Unmöglichkeit! Dieser Bogen ist auf beiden Seiten bedruckt: Einmal mit einer indischen Tempeltänzerin in schwarz – weiß, hinten dagegen die gleiche Tänzerin in bunt. Wieder ausschneiden und zusammensetzen: Vorne (nur schwarze Umrisslinien) stimmt das Bild. Logisch! Alles umdrehen und die bunten Teile zusammensetzen. Die gleiche Dame, die gleichen Teile – aber jetzt fehlt der Kopf!!! Mit diesem unglaublichen Rätsel können Sie Kinder, Jugendliche und Erwachsene stunden- und tagelang beschäftigen! Wie ist das möglich? Das Puzzle erinnert natürlich an andere „mathematisches Wunder“ von Sam Loyd (s.o.), die sich mit dem sog. geometrischen Verschwinden befassen …; aber diese Ausführung hier halten wir für besonders raffiniert und vor allem schön. Wenig Gepäck – Rieseneffekt! Staffelpreise: 1 – 9 Bögen: 2,50 € / Bogen 10 – 19 Bögen: 2,30 € 20 – 49 Bögen: 2,10 € ab 50 Bögen: 1,90 €
DAS gibt es in ganz Europa nur bei uns! Ein A 4 – Kartonbogen mit vier Exemplaren einer mathematischen Unmöglichkeit! Dieser Bogen ist auf beiden Seiten bedruckt: Einmal mit einer indischen Tempeltänzerin in schwarz – weiß, hinten dagegen die gleiche Tänzerin in bunt. Wieder ausschneiden und zusammensetzen: Vorne (nur schwarze Umrisslinien) stimmt das Bild. Logisch! Alles umdrehen und die bunten Teile zusammensetzen. Die gleiche Dame, die gleichen Teile – aber jetzt fehlt der Kopf!!! Mit diesem unglaublichen Rätsel können Sie Kinder, Jugendliche und Erwachsene stunden- und tagelang beschäftigen! Wie ist das möglich? Das Puzzle erinnert natürlich an andere „mathematisches Wunder“ von Sam Loyd (s.o.), die sich mit dem sog. geometrischen Verschwinden befassen …; aber diese Ausführung hier halten wir für besonders raffiniert und vor allem schön. Wenig Gepäck – Rieseneffekt! Staffelpreise: 1 – 9 Bögen: 2,50 € / Bogen 10 – 19 Bögen: 2,30 € 20 – 49 Bögen: 2,10 € ab 50 Bögen: 1,90 €
. .
„DAS TIER IN DEINEM KOPF IST …“ (Animal Magnetism) 6,50 € nur noch 5.- €!  Dieses einfach durchzuführende, absolut „übersichtliche“ und optisch schöne Mentalkunststück ist erschlagend und nicht zu durchschauen: Vier Zuschauer denken völlig frei an je ein Tier aus vier Karten mit jeweils vier Tieren. Kurze Zeit später kann der Zauberer angeben, welches Tier in welchem Kopf ist …! Die Tricktechnik basiert auf einem klassischen Kartenkunststück, ist hier aber so raffiniert überdeckt, dass nicht einmal die Kenner des ursprünglichen Tricks sie entdecken. MatheMagie ist die Grundlage …! Kein Kinderspielzeug!
Dieses einfach durchzuführende, absolut „übersichtliche“ und optisch schöne Mentalkunststück ist erschlagend und nicht zu durchschauen: Vier Zuschauer denken völlig frei an je ein Tier aus vier Karten mit jeweils vier Tieren. Kurze Zeit später kann der Zauberer angeben, welches Tier in welchem Kopf ist …! Die Tricktechnik basiert auf einem klassischen Kartenkunststück, ist hier aber so raffiniert überdeckt, dass nicht einmal die Kenner des ursprünglichen Tricks sie entdecken. MatheMagie ist die Grundlage …! Kein Kinderspielzeug!
.
.
.
.
. .
.BLITZRECHNER (Mathemagic) 6,00 €  Früher als „Steinzeitcomputer“ bekannt, mit dem auch ein Kind schneller rechnen kann als ein elektronischer Rechner! Vier mit Zahlen versehene, quadratische Stäbchen können in –zig verschiedenen Arten nebeneinandergelegt und gedreht werden. Sofort kann der Zauberer die Summe der vier vierstelligen Zahlen angeben! Ein raffiniertes mathematisches Prinzip steckt dahinter … Ab 8 Jahren bis 108 (mindestens) Auf YouTube gibt es (natürlich …) auch DAZU ein Filmchen (freundlicherweise ohne Lösung …): https://www.youtube.com/watch?v=MdbP_J3z5u8
Früher als „Steinzeitcomputer“ bekannt, mit dem auch ein Kind schneller rechnen kann als ein elektronischer Rechner! Vier mit Zahlen versehene, quadratische Stäbchen können in –zig verschiedenen Arten nebeneinandergelegt und gedreht werden. Sofort kann der Zauberer die Summe der vier vierstelligen Zahlen angeben! Ein raffiniertes mathematisches Prinzip steckt dahinter … Ab 8 Jahren bis 108 (mindestens) Auf YouTube gibt es (natürlich …) auch DAZU ein Filmchen (freundlicherweise ohne Lösung …): https://www.youtube.com/watch?v=MdbP_J3z5u8
Entweder kopieren sie dies und fügen es per Hand ein oder geben das Stichwort „Mental Log Inglese“ ein. Achtung: Nicht für Kinder unter drei Jahren geeignet
.
..
.ALKOHOL – TESTER (???) 4,50 € 
Ein ungeheuer verblüffender Effekt, der für viele Leute (auch hochgebildete!) unerklärlich ist! Betrachtet man den Namen von Worten „ohne Alkohol“ durch einen kleinen Glasstab, passiert gar nichts. Bei Whisky, Rum oder Champagner dagegen stehen diese Namen auf einmal auf dem Kopf. Geht auch mit bestimmten deutschen Wörtern …; funktioniert automatisch! Ideal für die Kneipentheke, den Stammtisch, den Biologie- (?), Physik- (!!! ) und vor allem den Mathematik (!!!!) – Unterricht …; wenig Gepäck, viel Staunen und Rätseln! Achtung: Nicht für Kinder unter drei Jahren geeignet
ACHTUNG: Extra für uns hat unser indischer Hersteller noch eine Neuauflage gemacht! Danach gibt es den AT nicht mehr!
.
.
.
.
Der Super – Blitzrechner (Improved Mental Logs) 20,50 €
 Ein Zuschauer kann vier massive, quadratische Metallstäbe (mit jeweils vier eingravierten Zahlen auf allen Seiten) beliebig so zusammenlegen, dass vier vierstellige Zahlen entstehen. Er soll dann deren Summe ermitteln. Dafür kann er sogar einen Taschenrechner verwenden. Bevor er die erste Zahl eingetippt hat, kann der Vorführende bereits das Ergebnis nennen. Damit noch nicht genug: Sogar die Summe der Zahlen auf der Rückseite (die zu keiner Zeit sichtbar waren!) kann sofort genannt werden. Und das bei Tausenden von Möglichkeiten! Es ist auch möglich, nur einen, zwei oder drei Stäbe zu verwenden. Immer genügt ein einziger Blick des Vorführenden, um die Summe der Zahlen anzugeben. Beliebig oft zu wiederholen – immer mit anderem Ergebnis! Ein edel gemachtes Requisit! Auch für Mathematiker nicht zu durchschauen! Sollte jeder Mathematiklehrer eigentlich immer bei sich haben … 🙂 Kein Kinderspielzeug!
Ein Zuschauer kann vier massive, quadratische Metallstäbe (mit jeweils vier eingravierten Zahlen auf allen Seiten) beliebig so zusammenlegen, dass vier vierstellige Zahlen entstehen. Er soll dann deren Summe ermitteln. Dafür kann er sogar einen Taschenrechner verwenden. Bevor er die erste Zahl eingetippt hat, kann der Vorführende bereits das Ergebnis nennen. Damit noch nicht genug: Sogar die Summe der Zahlen auf der Rückseite (die zu keiner Zeit sichtbar waren!) kann sofort genannt werden. Und das bei Tausenden von Möglichkeiten! Es ist auch möglich, nur einen, zwei oder drei Stäbe zu verwenden. Immer genügt ein einziger Blick des Vorführenden, um die Summe der Zahlen anzugeben. Beliebig oft zu wiederholen – immer mit anderem Ergebnis! Ein edel gemachtes Requisit! Auch für Mathematiker nicht zu durchschauen! Sollte jeder Mathematiklehrer eigentlich immer bei sich haben … 🙂 Kein Kinderspielzeug!
.
Sie waren eben auf unserer ersten MatheMagie – Seite! Weitere „Wunder“ folgen natürlich auf …
. .
| Seiten | 1 | 2 | 3 |
